Programação Concorrente e Distribuída
Esta página tem como objetivo apresentar a resolução das listas de exercícios do livro "An Introduction to Parallel Programming" de Peter Pacheco. A resolução dessas listas foi utilizada durante o curso de Programação Paralela no DCA / UFRN.
Respostas dos capítulos:
-
Chapter 01 - Why Parallel Computing?
Chapter 01 - Why Parallel Computing?
1.1 Devise formulas for the functions that calculate my first i and my last i in the global sum example. Remember that each core should be assigned roughly the same number of elements of computations in the loop. Hint: First consider the case when n is evenly divisible by p.
No raciocínio, foi considerado que o intervalo é fechado em my_first_i e aberto em
my_last_i.
A ocasião em que n é divisível por p é simples de formular, uma vez que o my_first_i é o
index do núcleo multiplicado pela divisão entre n e p.
As distribuições são iguais nessa situação, então o my_last_i será igual ao
my_first_i somado a divisão n/p.
No caso em que n não é divisível por p é necessário um maior tratamento.
Nessa situação, o resto da divisão tem que ser distribuído entre os outros núcleos. No máximo n - 1
(maior resto possível) itens serão distribuídos.
1.2 We’ve implicitly assumed that each call to Compute next value requires roughly the same amount of work as the other calls. How would you change your answer to the preceding question if call i = k requires k + 1 times as much work as the call with i = 0? So if the first call (i = 0) requires 2 milliseconds, the second call (i = 1) requires 4, the third (i = 2) requires 6, and so on.
Nessa situação, nota-se que o custo de cada requisição do compute next cresce a uma constante multiplicada por 2i. Uma estratégia que poderia ser tomada nessa situação (talvez não a melhor) seria fazer com que a quantidade de elementos que cada núcleo executaria seria metade dos elementos faltantes. Por exemplo, para n = 20 e p = 4, o primeiro nucleo executaria os 10 primeiros, o segundo núcleo executaria os 5 seguintes, o terceiro núcleo os 3 seguintes e o último núcleo os 2 restantes. Nessa situação apresentada, considerando um custo inicial de 2, os custos totais tomados por cada núcleo seria: 110, 130, 102 e 78.
Considere agora n =5 e p = 2. Os custos seriam: 2 4 6 8 10, respectivamente. Seguindo a lógica anterior, o primeiro núcleo executaria os índices: 0 , 1 e 2. E o segundo executaria os índices 3 e 4. Os custos totais seriam dessa situação seriam: 12 e 18, respectivamente, para cada núcleo.
1.3 Try to write pseudo-code for the tree-structured global sum illustrated in Figure 1.1. Assume the number of cores is a power of two (1, 2, 4, 8, . . . ). Hints: Use a variable divisor to determine whether a core should send its sum or receive and add. The divisor should start with the value 2 and be doubled after each iteration. Also use a variable core difference to determine which core should be partnered with the current core. It should start with the value 1 and also be doubled after each iteration. For example, in the first iteration 0 % divisor = 0 and 1 % divisor = 1, so 0 receives and adds, while 1 sends. Also in the first iteration 0 + core difference = 1 and 1 − core difference = 0, so 0 and 1 are paired in the first iteration.
divisor = 2;
coreDifference = 1;
jaEnviou = false;
for (i = 0; i < log(p) base 2; i++ ) { // 3 iterações para p = 8
if (indexCore % divisor == 0) {
// receba e some de (indexCore + coreDifference);
} else {
if ( ! jaEnviou) { // Nao envie caso já tenha enviado numa iteração anterior
// envie para (indexCore - coreDiffrence);
jaEnviou = true;
}
}
divisor *= 2;
coreDifference *= 2;
}
1.4 As an alternative to the approach outlined in the preceding problem, we can use C’s bitwise operators to implement the tree-structured global sum. In order to see how this works, it helps to write down the binary (base 2) representation of each of the core ranks, and note the pairings during each stage:[...] From the table we see that during the first stage each core is paired with the core whose rank differs in the rightmost or first bit. During the second stage cores that continue are paired with the core whose rank differs in the second bit, and during the third stage cores are paired with the core whose rank differs in the third bit. Thus, if we have a binary value bitmask that is 0012 for the first stage, 0102 for the second, and 1002 for the third, we can get the rank of the core we’re paired with by “inverting” the bit in our rank that is nonzero in bitmask. This can be done using the bitwise exclusive or ∧ operator. Implement this algorithm in pseudo-code using the bitwise exclusive or and the left-shift operator.
// indexNucleoPar refere-se ao array de bits que o núcleo atual irá ficar pareado
if (estagio == 1) {
indexNucleoPar[2] = indexAtual[2];
indexNucleoPar[1] = indexAtual[1];
if (indexAtual[0] ^ 1 ) {
// isso é verdade qnd o 3 bit do indexAtual for diferente de 1
indexNucleoPar[0] = 1;
} else {
indexNucleoPar[0] = 0;
}
}
if (estagio == 2) {
indexNucleoPar[0] = indexAtual[0];
indexNucleoPar[2] = indexAtual[2];
if (indexAtual[1] ^ 1 ) {
// isso é verdade qnd o 2 bit do indexAtual for diferente de 1
indexNucleoPar[1] = 1;
} else {
indexNucleoPar[1] = 0;
}
}
if (estagio == 3) {
indexNucleoPar[1] = indexAtual[1];
indexNucleoPar[0] = indexAtual[0];
if (indexAtual[2] ^ 1 ) {
// isso é verdade qnd o 1 bit do indexAtual for diferente de 1
indexNucleoPar[2] = 1;
} else {
indexNucleoPar[2] = 0;
}
}
1.5 What happens if your pseudo-code in Exercise 1.3 or Exercise 1.4 is run when the number of cores is not a power of two (e.g., 3, 5, 6, 7)? Can you modify the pseudo-code so that it will work correctly regardless of the number of cores?
Se o número de núcleos não forem uma potência de 2, eles não conseguirão ser pareados em toda e qualquer iteração da soma. Caso o número de núcleos seja 6, por exemplo, os núcleos poderão ser pareados na primeira iteração, mas na segunda iteração não, pois 3 não é divisível por 2. Uma possível alteração do código em 1.3 que resolveria esta situação seria a seguir:
divisor = 2;
coreDifference = 1;
jaEnviou = false;
qtdCoresExecucao= // NUMERO TOTAL DE CORES DO SISTEMA;
// qtdCoresExecucao refere-se a quantidade de núcleos que está em execução em cada iteração
for (i = 0; i < log(p) base 2; i++ ) { // 3 iterações, para 8 núcleos por exemplo
if (indexCore % divisor == 0 && indexCore + 1 != qtdCoresExecucao) {
// Recebem as somas parciais aqueles q são múltiplos de potência de 2 e cujos
//índices não é o ultimo dos cores em execução
// receba e some de (indexCore + coreDifference);
if (qtdCoresExecucao % 2 != 0 && indexCore == qtdCoresExecucao - 2) {
/* Caso a quantidade de cores que estão em execução nesta iteração não seja
múltipla de 2, o último core responsável por receber as somas deverá receber
também a soma parcial do core que “sobra”. O índice desse core é
qtdCoresExecucao -1.*/
// receba e some de (qtdCoresExecucao - 1)
}
} else {
if ( ! jaEnviou) { // Nao envie caso já tenha enviado numa iteração anterior
if (qtdCoresExecucao % 2 != 0 && indexCore + 1 == qtdCoresExecucao) {
/* Caso a quantidade de cores que estão em execução nesta iteração não
seja múltipla de 2 e o core atual for aquele que “sobra” no pareamento,
então envie para (indexCore - coreDifference - 1);*/
// envie para (indexCore - coreDiffrence -1);
} else {
// Caso contrário, execute o algoritmo normalmente como era antes
// envie para (indexCore - coreDiffrence);
}
jaEnviou = true;
}
}
divisor *= 2;
coreDifference *= 2;
qtdCoresExecucao-= 2^i; // O seu valor é reduzido em potência de 2
}
1.6 Derive formulas for the number of receives and additions that core 0 carries out using
a. the original pseudo-code for a global sum
No código original da soma global, o núcleo 0 receberá o resultado de cada cada um dos núcleo e somará cada um deles, logo a quantidade de dados recebidos será igual a quantidade de somas realizadas. Assim, a quantidade total será dada por: QtdSomas = (n - 1); onde n é o número de elementos que o núcleo irá processar.
b. the tree-structured global sum.
Já considerando a soma global em árvore estruturada (considerando número de núcleos sendo uma potência de 2), o núcelo 0 receberá o valor das somas parciais e somará, obtendo o valor total. Portanto a quantidade de números recebidos e adicionados serão iguais no entanto menor do que o do código original. Para dois núcleos, o resultado será 1, para 4 será 2, para 8 será 3, então, isso pode ser determinado pela seguinte fórmula: QtdSomas = QtdRecebidos =log2 (p)
Make a table showing the numbers of receives and additions carried out by core 0 when the two sums are used with 2, 4, 8,..., 1024 cores.
| Qtd Núcleos | Soma Global | Soma Árvore |
|---|---|---|
| 2 | 1 | 1 |
| 4 | 3 | 2 |
| 8 | 7 | 3 |
| 16 | 15 | 4 |
| 32 | 31 | 5 |
| 64 | 63 | 6 |
| 128 | 127 | 7 |
| 256 | 255 | 8 |
| 512 | 511 | 9 |
| 1025 | 1023 | 10 |
1.7 The first part of the global sum example—when each core adds its assigned computed values—is usually considered to be an example of data-parallelism, while the second part of the first global sum—when the cores send their partial sums to the master core, which adds them—could be considered to be an example of task-parallelism. What about the second part of the second global sum—when the cores use a tree structure to add their partial sums? Is this an example of data- or task-parallelism? Why?
Seria um exemplo de ambos conceitos, porque os núcleos compartilham tanto o dado compartilhado (suas somas parciais) quanto a tarefa em si, isto é, a tarefa de realizar a soma, a qual cada núcleo fica responsável por realizar parte dela.
1.8 Suppose the faculty are going to have a party for the students in the department.
a. Identify tasks that can be assigned to the faculty members that will allow them to use task-parallelism when they prepare for the party. Work out a schedule that shows when the various tasks can be performed.
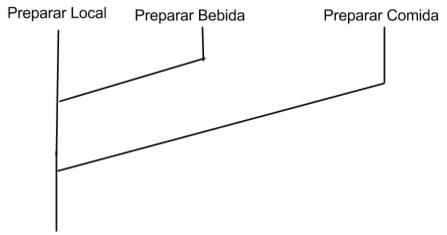
As tarefas de preparar o local, preparar a bebida e comida podem ser realizadas de forma paralela. Quando a bebida e a comida estão prontas, são trazidas até o local.
b. We might hope that one of the tasks in the preceding part is cleaning the house where the party will be held. How can we use data-parallelism to partition the work of cleaning the house among the faculty?
O dado compartilhado poderia ser o local ou os materiais (talheres, pratos e copos) que estariam sendo utilizados tanto pelo pessoal da festa, quanto pelos da limpeza.
c. c. Use a combination of task- and data-parallelism to prepare for the party. (If there’s too much work for the faculty, you can use TAs to pick up the slack.)
As duas tarefas seriam o pessoal da festa estaria requisitando a utilização dos materiais, e a outra tarefa paralela estaria sendo responsável por pegar aqueles materiais que já foram usados e limpá-los. Sendo que as duas tarefas não poderiam estar compartilhando o mesmo recurso (devem solicitar lock).
1.9 Write an essay describing a research problem in your major that would benefit from the use of parallel computing. Provide a rough outline of how parallelism would be used. Would you use task- or data-parallelism?
Um exemplo de problema que seria beneficiado com a utilização de paralelismo seria a de movimentação de dinheiro em uma conta bancária. O tipo de paralelismo nenessário nesse problema seria o de data. Por exemplo, caso haja a execução de duas transações ao mesmo tempo como depósito e saque, o acesso ao saldo atual do usuário deveria ser sincronizado. Por exemplo:
float saldo;
void saque(float saque) {
float saldoAtual = saldo;
saldo = saldoAtual - saque;
}
void deposito(float deposito) {
float saldoAtual = saldo;
saldo = saldoAtual + deposito;
}
O acesso ao valor da variável saldo deveria ser realizado de forma sincronizada. No exemplo acima, caso as duas funções fossem executadas ao mesmo tempo, poderia ocorrer a situação em que o saldoAtual em ‘deposito’ teria o valor antes de ser executado o saque. Assim, o valor do saldo que seria armazenado seria incorreto.